O framework AHP ou Processo Hierárquico Analítico, é um métodos de tomada de decisão com vários critérios (MCDM), desenvolvido por por Thomas L. Saaty na década de 1970, e é muito utilizado para organizar e analisar decisões complexas, usando matemática e psicologia.
Ao reduzir decisões complexas a uma série de comparações e depois sintetizar os resultados, o AHP ajuda a capturar os aspectos subjetivos e objetivos de uma decisão. O AHP tamébm incorpora uma técnica útil para verificar a consistência das avaliações do tomador de decisão, reduzindo assim o viés no processo de tomada de decisão.
Vamos filosofar um pouco: a vida é composta de uma quantidade infinita de opções. A maioria das decisões, como a que você vai almoçar hoje, é pequena e tem pouco impacto na sua vida. Mas existem aquelas decisões, aquelas realmente importantes que podem ter um grande impacto na sua vida!
Ok, chega de filosofia! Deixa eu te perguntar algumas coisas: qual o seu processo para tomar decisões? DACI? RAPID? Outro processo? E se você é um gerente de produto / projeto, como você decide quais projetos e features investir?
Foi exatamente isso que Thomas L. Saaty se questionou quando ele criou o AHP, ou Processo Hierárquico Analítico. Para Saaty nossas vidas são o somatório de nossas decisões. Seja na esfera dos negócios ou na vida pessoal. A forma como as decisões são realizadas é tão importante quanto o que será decidido, afinal de contas, a escolha precisa ser feita, e uma abordagem sistêmica e compreensiva é necessária para a tomada de decisão.
O objetivo deste artigo é apresentar, discutir e aplicar os princípios e técnicas do processo de hierarquia analítica (AHP) na tomada de decisões, com exemplos de como você pode aplicar na escolha de projetos a serem desenvolvidos. O AHP é um dos principais modelos matemáticos atualmente disponíveis para apoiar a teoria da decisão.
Nota: nesse artigo vamos mostrar como utilizar o AHP no mundo comporativo, especificamente, na escolha de projetos que serão desenvolvidos, mas você pode utilizar o framework em todos os aspectos da sua vida.
O que é o AHP ou Processo Hierárquico Analítico?
“Decretos dos Princípios Matemáticos” ou “Princípios Matemáticos da Tomada de Decisão” é o título do livro do Prof. Thomas L. Saaty, no qual ele descreve seu método para o tratamento matemático de problemas de decisão, que ele desenvolveu nos anos 70, o AHP. Desde sua introdução o framework evolui muito e atualmente é utilizado em todo o mundo em muitos campos diferentes.
AHP significa “Processo Hierárquico Analítico” e pertence ao grupo de métodos de tomada de decisão com múltiplos critérios (MCDM). No AHP, valores como preço, peso ou área, ou mesmo opiniões subjetivas, como sentimentos, preferências ou satisfação, podem ser traduzidos em relações numéricas mensuráveis.
O método é extensivamente estudado e atualmente é usado na tomada de decisões em cenários complexos, onde as pessoas trabalham juntas para tomar decisões quando percepções, julgamentos e conseqüências humanas têm repercussões a longo prazo.
O método AHP analisa o problema em três partes:
- A primeira parte e a questão que precisa ser resolvida;
- A segunda parte, são “as soluções alternativas disponíveis para resolver o problema;
- A terceira e a parte mais importante, no que diz respeito ao método AHP, são os critérios utilizados para avaliar as soluções alternativas. Embora existam vários critérios, a magnitude de cada critério pode não ser igual.
Por exemplo, se você tiver que escolher entre dois restaurantes, o sabor e o tempo de espera são dois fatores; no entanto, ambos podem não ter a mesma importância em sua percepção. O sabor pode ser muito mais importante do que o tempo de espera e assim por diante. Portanto, se você atribuir peso 2 a gosto e 1 a tempo de espera, é mais provável que você chegue a um restaurante que melhor atenda às suas necessidades.
Ao avaliar soluções alternativas, é necessário anexar pesos aos critérios para garantir a conclusão correta. Isso pode parecer óbvio, mas durante muito tempo os gerentes enfrentam problemas de como atribuir pesos.
Vantagens e desvantagens do framework AHP
• Vantagens
- Facilidade no entendimento. O AHP permite que o usuário atribua pesos relativos para múltiplos critérios, de forma intuitiva, ao mesmo tempo em que realiza uma comparação par a par entre os mesmos. Isso permite que, mesmo quando duas variáveis são incomparáveis, com os conhecimentos e a experiência das pessoas, pode-se reconhecer qual dos critérios é mais importante.
- Qualitativo e quantitativo. Os valores dos julgamentos das comparações pares são baseados em experiência, intuição e também em dados físicos, dessa forma, o AHP permite comparar aspectos qualitativos e quantitativos de um problema de decisão.
- Redundâncias para melhorar os dados. Por reconhecer que participantes podem estar incertos ou fazer julgamentos pobres em algumas comparações, o método de Saaty envolve comparações redundantes para melhorar a validade destas. Nota: a tolerância de inconsistências não é uma limitação, mas um retrato da realidade.
- Excelente para tomar decisões sobre um grande número de opções. Para mim, a principal vantagem é o fato do AHP permitir comparar e avaliar dezenas de critérios, sub-critérios, e opções de forma relativamente simplificada (vou mostrar seu funcionamento a seguir)
Assim, a aplicação do AHP inclui e mede todos os fatores importantes, qualitativa e quantitativamente mensuráveis, sejam eles tangíveis ou intangíveis, para aproximar-se de um modelo realistas
• Desvantagens
- Precisa de hierarquia dos dados. Uma das principais características do AHP, é que ele utiliza da hierarquia dos critérios que precisam ser decididos. Com isso, nem toda tomada de decisão é possível construir essa hierarquia de informações.
- Difícil utilização. Apesar da facilidade em entender como aplicar o AHP, sua utilização é complexa, envolvendo muitos passos, como – construir a hierarquia, comparar os diversos critérios e subcriterios, verificar se os dados são consistentes, dentre outros.
Como podemos ver, as desvantagens são muito inferiores as grandes vantagens que o framework proporciona. E mesmo nos pontos listados acima, nós temos maneiras de contorna-las, você pode utilizar um planilha simples para executar o framework (como vou mostrar a seguir), ou utilizar alguma ferramenta especializada.
As aplicacões do framework AHP
Existem diversas aplicações comprovadas para o framework AHP quando falamos sobre situações de decisão complexas, desde problemas envolvendo planejamento, alocação de recursos, definindo prioridades e seleção de alternativas..
Essa lista não é exaustiva, podendo também citar, previsão, gerenciamento de qualidade, reengenharia de processos de negócios, implantação de função de qualidade e o scorecard, e claro, o meu preferido: priorização de features e projetos.
Outras aplicações comuns são:
- Selecione um tipo de reatores nucleares;
- Decidindo a melhor forma de reduzir o impacto das mudanças climáticas globais;
- Quantificando a qualidade geral dos sistemas de software;
- Selecionando faculdade universitária;
- Decidindo onde localizar plantas de fabricação offshore;
- Avaliando o risco na operação de tubulações de petróleo de todo o país;
- Decidindo a melhor maneira de gerenciar as bacias hidrográficas;
A aplicação do framework AHP é extensa (e confesso que acho que infinita) devido a sua versatilidade e uso de estruturas hierárquicas. Então lembre-se: se precisar avaliar diferentes critérios em diversas categorias e opções, o framework AHP pode ser a melhor alternativa.
Mas como estruturar o framework AHP? Boa pergunta, vamos falar disso agora…
A estrutura do framework AHP
A aplicação do framework AHP começa com um problema sendo decomposto em uma hierarquia de critérios, para ser mais facilmente analisado e comparado de maneira independente. Depois que essa hierarquia lógica é construída, os tomadores de decisão podem avaliar sistematicamente as alternativas fazendo comparações aos pares para cada um dos critérios escolhidos.
Segundo Saaty, essa comparação pode utilizar dados concretos ou julgamentos subjetivos como uma maneira de inserir as informações.
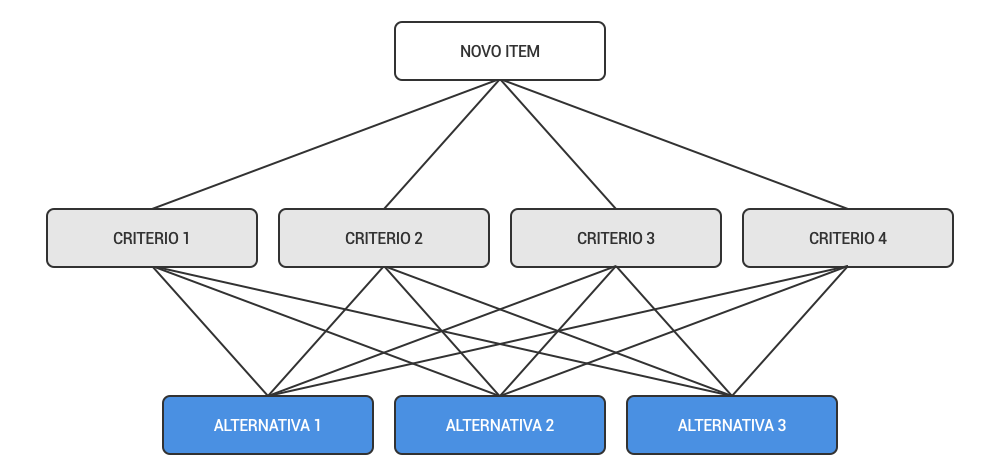
O AHP transforma as comparações, que geralmente são empíricas, em valores numéricos que são posteriormente processados e comparados. O peso de cada fator permite a avaliação de cada um dos elementos dentro da hierarquia definida.
Depois que todas as comparações foram feitas e os pesos relativos entre cada um dos critérios a serem avaliados foram estabelecidos, a probabilidade numérica de cada alternativa é calculada. Essa probabilidade determina a probabilidade de a alternativa cumprir o objetivo esperado. Quanto maior a probabilidade, maiores as chances de a alternativa satisfazer o objetivo final.
A estrutura que o framework AHP segue é basicamente:
- Defina o objetivo da decisão – o que eu quero decidir, com que finalidade e quais são minhas alternativas?
- Estruturar o problema de decisão em uma hierarquia – quais são as categorias e critérios que figuram na minha decisão?
- Parear a comparação de critérios em cada categoria – por exemplo, azul ou verde? Qual eu prefiro e quanto prefiro uma ou outra cor?
- Calcular as prioridades e um índice de consistência – minhas comparações foram lógicas e consistentes?
- Avalie alternativas de acordo com as prioridades identificadas – que solução ótima alternativa existe para o problema de decisão?
O cálculo matemático envolvido no processo de AHP pode parecer simples, mas ao lidar com casos mais complexos, as análises e cálculos se tornam mais profundos e mais exaustivos.
Importante: O núcleo do AHP é a comparação de pares em vez de ordenar (classificação), votar (por exemplo, atribuir pontos) ou atribuir gratuitamente prioridades. A validação do método em testes práticos mostra uma concordância surpreendentemente boa com os valores reais medidos.
Exemplo prático do funcionamento do AHP
Embora o AHP seja um dos métodos mais avançados disponíveis no campo da ciência de gerenciamento e pesquisa operacional, sua aplicação exige algumas etapas que são trbalhasosas. Mas como citado anteriormente, você pode utilizar software e uma planilha simples.
Vou exemplificar nos pontos a seguir, seu funcionamento e como você pode aplica-lo utilizando uma planilha.
Etapa 1 – Definir alternativas e os critérios
O processo do AHP começa definindo as alternativas que precisam ser avaliadas. Essas alternativas podem ser os diferentes critérios em que as soluções devem ser avaliadas. Eles também podem ser as diferentes features de um produto que precisam ser ponderados para entender melhor a percepção do cliente. No final da etapa 1, uma lista abrangente de todas as alternativas disponíveis deve estar pronta.
Por exemplo: vamos decidir qual projeto feature vamos desenvolver baseada em alguns critérios, como: valor, impacto, complexidade. O diagrama abaixo representa o que será feito:
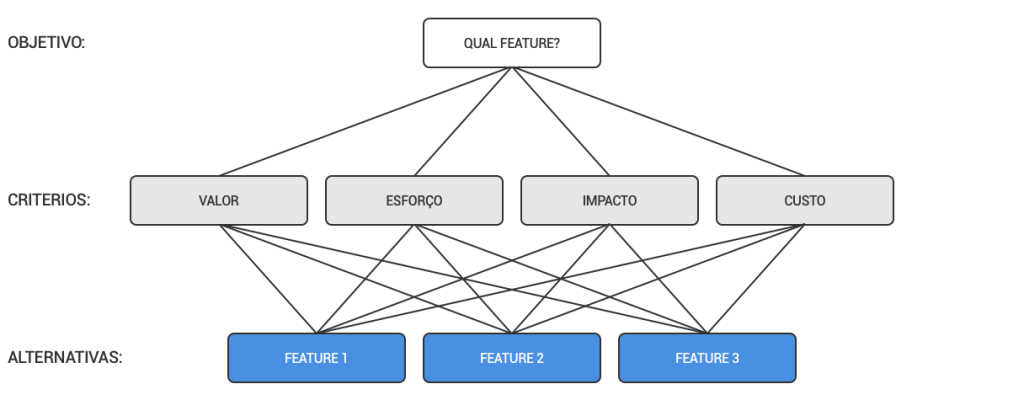
| Feature / Projeto | Valor | Esforço | Impacto | Custo |
|---|---|---|---|---|
| Feature 1 | 8 | 11 | 1.000 | $ 10.000 |
| Feature 2 | 5 | 5 | 2.000 | $ 3.000 |
| Feature 3 | 10 | 8 | 500 | $ 8.000 |
Os valores listados na tabela acima, foram levantados de uma analise feita previamente, cada um de sua maneira:
- Valor: pesquisa realizada com os clientes, onde eles precisavam dar uma nota de 1 a 10 para cada feature;
- Esforço: horas/homem necessárias para desenvolver essa feature;
- Impacto: tamanho da base que vai se beneficiar com essa feature;
- Investimento: investimento necessário para desenvolver a feature;
Etapa 2 – Determinando a matriz de comparação
Após o estabelecimento da hierarquia, os critérios devem ser avaliados em pares, a fim de determinar a importância relativa entre eles e seu peso relativo ao objetivo global. A comparação entre dois elementos usando AHP pode ser feita de maneiras diferentes, no entanto, a escala de importância relativa entre duas alternativas, como sugerido por Saaty, é a mais utilizada.
Atribuindo valores que variam de 1 a 9, a escala determina a importância relativa de uma alternativa quando comparada com outra alternativa, como podemos ver na tabela abaixo:
| Escala | Explicação | Valor | Reciprova |
|---|---|---|---|
| Mesma importância | As duas atividades contribuem igualmente para o objetivo. | 1 | 1 |
| Intermediario | 2 | 1/2 | |
| Importância pequena de uma sobre a outra | A experiência e o julgamento favorecem levemente uma atividade em relação à outra. | 3 | 1/3 |
| Intermediario | 4 | 1/4 | |
| Importância grande ou essencial | A experiência e o julgamento favorecem fortemente uma atividade em relação à outra. | 5 | 1/5 |
| Intermediario | 6 | 1/6 | |
| Importância muito grande ou demonstrada | Uma atividade é muito fortemente favorecida em relação à outra; sua dominação de importância é demonstrada na prática. | 7 | 1/7 |
| Intermediario | 8 | 1/8 | |
| Importância absoluta | A evidência favorece uma atividade em relação à outra com o mais alto grau de certeza. | 9 | 1/9 |
É comum sempre usar números ímpares da tabela acima para garantir uma distinção razoável entre os pontos de medição. O uso de números pares somente deve ser adotado se houver necessidade de negociação entre os avaliadores. Quando um consenso natural não pode ser alcançado, aumenta a necessidade de determinar um ponto intermediário como a solução negociada.
Nota: a diagonal tem valor “1” porque a comparação de um elemento com ele mesmo, tem “igual valor”.
| Valor | Esforço | Impacto | Custo | |
| Valor | 1 | 1/5 | 1/9 | 1 |
| Esforço | 5 | 1 | 1 | 5 |
| Custo | 9 | 1 | 1 | 5 |
| Risco | 1 | 1/5 | 1/5 | 1 |
No exemplo acima, o esforço tem uma importância grande/maior, quando comparado ao valor, e por isso, sua nota é 5, e sua reciproca é 1/5.
Etapa 3 – Determinar o vetor de prioridade (eigenvector)
Para interpretar e atribuir pesos relativos a cada critério, é necessário normalizar a matriz de comparação anterior. A normalização é feita dividindo cada valor pelo valor total da coluna.
| Valor | Esforço | Impacto | Custo | |
| Valor | 1 | 1/5 | 1/9 | 1 |
| Esforço | 5 | 1 | 1 | 5 |
| Impacto | 9 | 1 | 1 | 5 |
| Custo | 1 | 1/5 | 1/5 | 1 |
| TOTAL | 16 | 2.4 | 2.31 | 12 |
| Valor | Esforço | Impacto | Custo | |
| Valor | 1/16 = 0.063 | 0.083 | 0.048 | 0.083 |
| Esforço | 5/16 = 0.313 | 0.417 | 0.433 | 0.417 |
| Impacto | 9/16 = 0.563 | 0.417 | 0.433 | 0.417 |
| Custo | 1/16 = 0.063 | 0.083 | 0.087 | 0.083 |
Dividimos cada célula pelo valor total da sua coluna
A contribuição de cada critério para a meta da empresa/projeto é determinada por cálculos feitos usando o vetor prioritário (ou Eigenvector). O vetor prioritário mostra os pesos relativos entre cada critério; é obtido de maneira aproximada, calculando a média matemática de todos os critérios, conforme mostrado abaixo.
Podemos observar que a soma de todos os valores do vetor é sempre igual a um (1).
| Calculo do vetor de prioridade (eigenvector) | vetor de prioridade | |
| Valor | [ 0.063 + 0.083 + 0.048 + 0.083 ] / 4 = 0.0693 | 0.0693 (6,93%) |
| Esforço | [ 0.313 + 0.417 + 0.433 + 0.417 ] / 4 = 0.3946 | 0.3946 (39,46%) |
| Impacto | [ 0.563 + 0.417 + 0.433 + 0.417 ] / 4 = 0.4571 | 0.4571 (45,71%) |
| Custo | [ 0.063 + 0.083 + 0.087 + 0.083 ] / 4 = 0.0789 | 0.0789 (7,89%) |
Os valores encontrados no valor de prioridade (eigenvector) têm um significado físico direto no AHP – eles determinam a participação ou o peso desse critério em relação ao resultado total da meta.
Por exemplo, em nosso exemplo, o critério “impacto” têm um peso de 45,71% em relação ao total. Uma avaliação positiva sobre esse fator contribui com aproximadamente 7 (sete) vezes mais que uma avaliação positiva no critério de valor (peso 6,93%).
Etapa 4 – Calcular indica de inconsistência
O próximo passo é procurar por inconsistências de dados. O objetivo é capturar informações suficientes para determinar se os tomadores de decisão foram consistentes em suas escolhas.
Por exemplo, se os tomadores de decisão afirmam que o critério “Impacto” é mais importante que o critério Esforço”” e que o critério “esforço” é mais importantes que o critério “custo” , seria inconsistente afirmar que o critérios “custo” é mais importante que o critério “impacto”. (se A> B e B> C, seria inconsistente que A <C).
O índice de inconsistência é baseado no valor próprio máximo, calculado pela soma do produto de cada elemento no vetor próprio pelo respectivo total da coluna da matriz de comparação original. Como por exemplo:
| Vetor de prioridade (eigenvector) | 0.0693 | 0.3946 | 0.4571 | 0.0789 |
| Total | 16 | 2.4 | 2.31 | 12 |
| Maximo eigenvector | [ (0.0693 * 16) + (0.3946 * 2.4) + (0.4571 * 2.31) + (0.0789 * 12) ] = 4.05 |
O cálculo do índice de consistência de Saaty é dado pela seguinte fórmula:
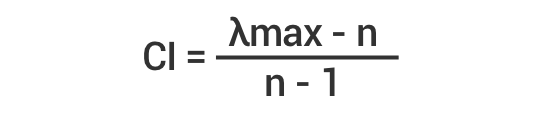
Onde CI é o índice de consistência e “n” é o número de critérios avaliados.
Para nosso exemplo, o índice de consistência (CI) é:
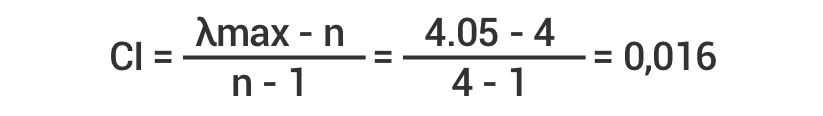
Etapa 5 – Verificar se o índice de consistência (IC) é adequado
Para verificar se o índice de consistência (CI) é adequado, Saaty sugere o que foi chamado de taxa de consistência (CR), que é determinada pela razão entre o índice de consistência e o índice de consistência aleatória (IR). A matriz será considerada consistente se a proporção resultante for menor que 10%.
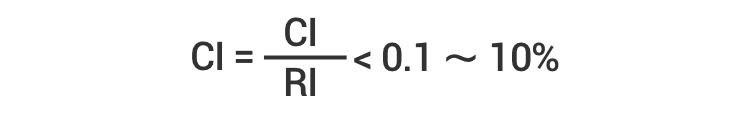
O valor do RI é fixo e é baseado no número de critérios avaliados, conforme mostrado na tabela abaixo:
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| RI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
Para nosso exemplo, a taxa de consistência para o grupo de critérios inicial é:
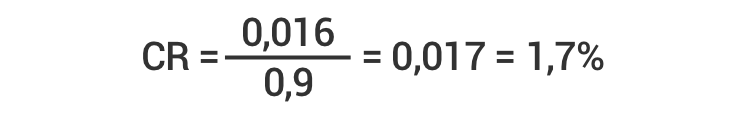
Como seu valor é inferior a 10%, a matriz pode ser considerada consistente.
E finalmente, na imagem abaixo podemos ver o quanto cada critério contribui / é importante para a priorização das features do nosso exemplo. Os valores “Impacto” e “Esforço” são muito mais importantes para nossa priorização do que os valores “Valor” e “Encanto”.

Etapa 6 – Pontuar os projetos
Essa é a ultima etapa do processo. Agora que você já tem os pesos, ou seja, o que considera mais importante ser avaliado no processo, é hora de verificar as características de cada feature/projeto avaliado. Como no nosso exemplo:
| Feature / Projeto | Valor | Esforço | Impacto | Custo |
|---|---|---|---|---|
| Feature 1 | 8 | 11 | 1.000 | $ 10.000 |
| Feature 2 | 5 | 5 | 2.000 | $ 3.000 |
| Feature 3 | 10 | 8 | 500 | $ 8.000 |
Para conseguirmos comparar as features e seus valores, para CADA característica, é preciso normalizar os valore. E se os valores forem inversamente proporcionais no ganho, ou seja, quanto menos, melhor; é preciso harmonizar antes. No nosso exemplo, isso acontece com os critérios “esforço” e “custo”.
- Normalizar: somar todos os valores da coluna e dividir cada célula pelo valor total
- Harmonizar: somar todos os valores da coluna e dividir esse valor pelo valor de cada célula;
| Feature / Projeto | Valor | Normalizada |
|---|---|---|
| Feature 1 | 8 | 8/23 = 0,34 = 34% |
| Feature 2 | 5 | 5/23 = 0,23 = 23% |
| Feature 3 | 10 | 10/23 = 0,43 = 43% |
| TOTAL | 23 |
| Feature / Projeto | Esforço | Harmonizar | Normalizada |
|---|---|---|---|
| Feature 1 | 11 | 24/11 = 2,2 | 2.2/10 = 0,22 = 22% |
| Feature 2 | 5 | 24/5 = 4,8 | 4,8/10 = 0,48 = 48% |
| Feature 3 | 8 | 24/8 = 3 | 3/10 = 0,3 = 30% |
| TOTAL | 24 | 10 |
Nota: como o critério “Esforço”é inversamente proporcional, ou seja, quanto menor, melhor; precisamos harmonizar antes de normalizar.
| Feature / Projeto | Impacto | Normalizada |
|---|---|---|
| Feature 1 | 1.000 | 1.000/3.500 = 0,28 = 29% |
| Feature 2 | 2.000 | 2.000 / 3.500 = 0,57 = 57% |
| Feature 3 | 500 | 500/3.500 = 0,14% |
| TOTAL | 3.500 |
| Feature / Projeto | Custo | Harmonizar | Normalizada |
|---|---|---|---|
| Feature 1 | $ 10.000 | 21.000/10.000 = 2,1 | 2,1/11,7 = 0,18 = 18% |
| Feature 2 | $ 3.000 | 21.000/3.000 = 7 | 7/11,7 = 0,60 = 60% |
| Feature 3 | $ 8.000 | 21.000/8.000 = 2,6 | 2,6/11,7 = 0,22 = 22% |
| TOTAL | $ 21.000 | 11,7 |
Nota: como o critério “Custo” é inversamente proporcional, ou seja, quanto menor, melhor; precisamos harmonizar antes de normalizar.
Agora que você tem todos os valores das features normalizadas para cada uma dos critérios que estamos levando com consideração na avaliação, basta fazer uma multiplicacão de matriz (vetor dos critérios X cada critério de cada feature).
Por exemplo, o valor do vetor de decisão da feature 1, será calculado da seguinte maneira:
- (34% * 6,93%) + (22% * 39,46%) + (28% * 45,71) + (18 * 7,89%) = 25%
O resultado – “vetor de decisão”, vai ser a ordenação / priorização que cada feature e/ou projeto deve ser desenvolvido, indo do que tiver maior porcentagem para o de menor porcentagem.
| Critérios | Valor | Esforço | Impacto | Risco | Vetor de Decisão |
|---|---|---|---|---|---|
| Vetor dos Critérios | 6,93% | 39,46 | 45,71 | 7,89% | — |
| Feature 1 | 34% | 22% | 28% | 18% | 25% |
| Feature 2 | 23% | 48% | 57% | 60% | 52% |
| Feature 3 | 43% | 30% | 14% | 22% | 23% |
Como podemos ver no resultado, a Feature 2 deve ser priorizada em primeiro lugar, em seguida a feature 1 e a feature 3.
Muito importante: no nosso exemplo, nós demos uma nota para cada fator associada a cada feature / projeto. Esse valor pode ser storypoints, tempo de desenvolvimento, votação dos clientes, etc.
O framework AHP e a Gestão de Produto
O framework AHP agrega valor no planejamento de um projeto, ao tratar de prioridades, de parâmetros ótimos e de seleção de alternativas. O AHP é baseado na nossa habilidade de fazer julgamentos sobre diversos critérios subjetivos e de combinar com critérios objetivos. (pesquisas, questionários, dados, etc).
Por isso, o framework pode ser utilizada na gestão de produtos/projetos: o AHP auxilia na tomada de decisão de qual projeto investir, ou qual feature desenvolver. E o para mim, o mais importantes, ele é muito útil quando você precisa tomar decisões sobre dezenas de features, com dezenas de critérios e sub-critérios a serem analisados.
O projeto avaliado na pesquisa tem diversas variáveis que dificultam a medição do desempenho. De fato, o AHP é útil no estudo em questão porque busca simplificar a medição, com sua capacidade de simplificar e organizar de forma racional os critérios necessários para a avaliação.
Ao considerar aspectos objetivos e subjetivos, numéricos e qualitativos, o método consegue compor um índice único formado pela combinação dos principais critérios do problema e das áreas de conhecimento de gerenciamento sugeridas gerente de produto.
Conclusão
O framework AHP ou Processo Hierárquico Analítico, vem atraindo o interesse de muitos pesquisadores e aumentado seu uso entre os gerentes de produto, principalmente devido às suas características matemáticas e ao fato de a entrada de dados ser bastante simples de ser produzida. Sua simplicidade é caracterizada pela comparação pareada das alternativas de acordo com critérios específicos
Sua aplicação simples para selecionar projetos/features para o portfólio permite que os tomadores de decisão tenham uma ferramenta específica e matemática de suporte à decisão. Essa ferramenta não apenas suporta e qualifica as decisões, mas também permite que os tomadores de decisão justifiquem suas escolhas, além de simular possíveis resultados.
Importante: a tomada de decisão assume uma compreensão macro do contexto que vai além da escolha de uma framework. A decisão sobre um produto/projeto que será desenvolvido é fruto de negociação entre os stakeholders, analise estratégica, em que o AHP ajuda e orienta, mas ela deve ser estar atrelada aos objetivos da empresa.
Espero que tenha gostado do artigo, e para finalizar, tenho algumas recomendações de outros tópicos importantes:
- Como priorizar features para seu roadmap – conheça outra frameworks para auxiulia-lo na decisão.
- O framework estratégico 3 horizontes de inovação para ajuda-lo a ter idéias de longo prazo e conecta-las com ações de médio prazo.

