Descrito pela primeira vez por Francis Galton, um diagrama de dispersão é usado para mostrar a relação entre dois tipos de dados. Pode ser a relação entre uma causa e um efeito, entre uma causa e outra, ou mesmo entre uma causa e duas outras.
Suponha que você esteja enfrentando um problema. Você seguiu as etapas do seu modelo de solução de problemas. Você definiu o problema usando o Gráfico de Pareto. Além disso, você analisou como o processo está se comportando usando diagramas de fluxo de processo, histogramas e gráficos de controle, etc.
O processo está sob controle, mas os resultados não são aceitáveis. Há muita variação no processo (ou talvez ele esteja operando em um nível ou média incorreta). Você precisa descobrir o que está fazendo com que o processo se comporte dessa forma.
Um diagrama de Ishikawa foi construído. Este diagrama lista algumas das possíveis causas do problema. Como você determina quais causas são responsáveis pela variação? Por exemplo, o rendimento da reação é mais influenciado pelo tempo de execução ou pressão?
Um método de fazer isso é usar um diagrama de dispersão (em inglês Scatter Diagrams), e é sobre ele que vamos discutir nesse artigo.
O que é o Diagrama de Dispersão
Descrito pela primeira vez por Francis Galton, um diagrama de dispersão é usado para mostrar a relação entre dois tipos de dados. Pode ser a relação entre uma causa e um efeito, entre uma causa e outra, ou mesmo entre uma causa e duas outras.
Se uma relação for identificada, então surge a possibilidade de que uma variável possa ser controlada pela variação da outra variável.
A principal vantagem do diagrama de dispersão reside na sua simplicidade. Mas é importante que todas as outras variáveis potenciais dentro de um processo sejam compreendidas, controladas e monitoradas para garantir que os resultados obtidos de quaisquer experimentos ou interpretação de um diagrama não sejam comprometidos.
Os diagramas de dispersão são uma forma de visualizar o relacionamento entre os dados: plotando os pontos desses dados, você obtém uma dispersão de pontos em um gráfico. A análise surge ao tentar discernir que tipo de padrão – se houver – está presente, e claro, o que esse padrão significa.
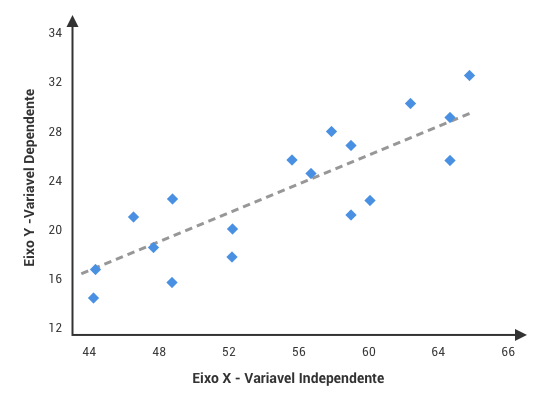
Os dados são exibidos como uma coleção de pontos, cada um com o valor de uma variável determinando a posição no eixo horizontal e o valor da outra variável determinando a posição no eixo vertical (em caso de duas variáveis
Exemplo do Diagrama de Dispersão
Suponha que você esta desenvolvendo um processo para te ajudar a chegar ao trabalho em um certo tempo.
O gráfico de controle que você construiu no processo mostra que, em média, você leva 25 minutos para chegar ao trabalho. Você gostaria de diminuir essa média para 20 minutos. Quais são as causas do processo que afetam o tempo que você leva para chegar ao trabalho?
Existem muitas causas possíveis, incluindo trânsito, a velocidade que você dirige, a hora que você sai para o trabalho, condições meteorológicas, etc. Suponha que você decidiu que a velocidade que você dirige é a causa mais importante. Um diagrama de dispersão pode ajudá-lo a determinar se isso é verdade.
Nesse caso, o diagrama de dispersão mostraria a relação entre uma “causa” e um “efeito”. A causa é a velocidade com que você dirige e o efeito é o tempo que leva para chegar ao trabalho. Você pode examinar essa relação de causa e efeito variando a velocidade com que dirige para o trabalho e medindo o tempo que leva para chegar ao trabalho.
Por exemplo, em um dia você pode dirigir a 40 km/h e medir o tempo que leva para chegar ao trabalho em minutos. No dia seguinte, você pode dirigir a 80 km/h e medir o tempo que leva para chegar ao trabalho. Depois de coletar dados suficientes, você pode traçar a velocidade que você dirige em relação ao tempo que leva para chegar ao trabalho.
| Rapidez | Tempo | Rapidez | Tempo |
|---|---|---|---|
| 64 | 17 | 48 | 29 |
| 62 | 23 | 59 | 14 |
| 51 | 26 | 57 | 18 |
| 46 | 28 | 50 | 22 |
| 52 | 27 | 45 | 23 |
| 51 | 28 | 47 | 32 |
| 57 | 20 | 46 | 22 |
| 60 | 14 | 61 | 24 |
| 55 | 17 | 54 | 25 |
| 51 | 21 | 53 | 24 |
| 64 | 15 | 45 | 31 |
| 60 | 24 | 54 | 25 |
| 61 | 19 |
A Figura 1 é um exemplo de diagrama de dispersão para este caso. A causa (velocidade) está no eixo x. O efeito (tempo que leva para chegar ao trabalho) está no eixo y. Cada conjunto de pontos emparelhados é traçado no diagrama de dispersão.
A linha contínua no gráfico é a linha de “melhor ajuste” que será discutida nos pontos a seguir.
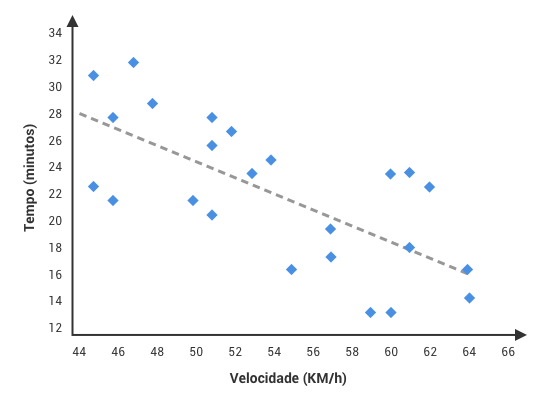
Dados de velocidade X tempo
Para entender se existe uma correlação entre os pontos, nós precisamos discutir e responder 2 perguntas:
- Existe uma correlação entre os pontos?
- A correlação é estatisticamente significativa?
São essas 2 perguntas que vamos responder e exemplificar abaixo.
Correlação do diagrama de dispersão
Quando criamos o gráfico, a primeira pergunta é realmente respondida olhando para o diagrama de dispersão e decidindo se há algum tipo de correlação. As figuras abaixo mostram os tipos gerais de relacionamentos que podem existir:
• Níveis de correlação
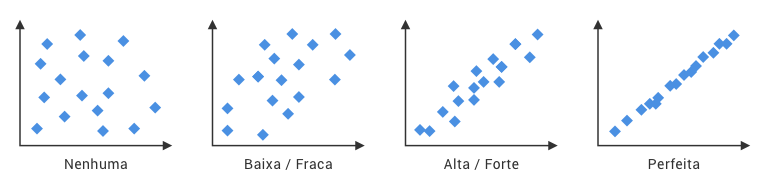
- Nenhuma. Nessa situacão, as 2 variaveis que estão sendo analisadas não possuem nenhuma correlação. O padrão parece um tipo de espingarda. No exemplo anterior, isso quer dizer que não importa sua velocidade, ela não é um fator que interfere na chegada ao trabalho.
- Alta / Forte. Quanto menor for a dispersão dos pontos (ou seja, mais proximos de uma reta), maior será a correlação entre os dados. Com isso, podemos identificar como forte quando os dados estão bem próximos, altamente concentrados.
- Baixa / Fraca. Então quanto maior for a dispersão dos pontos, menor será o grau de correlação entre os dados, ou seja, eles quase não possuem uma correlação.
- Perfeita. A correlação é perfeita quando não há uma grande dispersão entre os pontos, a correlação será total entre os dados, independente da tendência, seja ela positiva ou negativa.
• Tipos de correlação
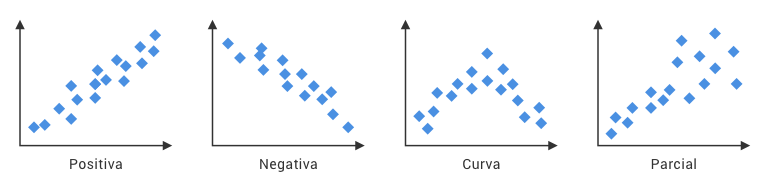
- Positiva. Este tipo de correlação acontece quando há uma tendência crescente entre os pontos. Conforme uma variável aumenta, a outra variável também aumenta proporcionalmente. No nosso exemplo, quanto mais rápido você dirige, mais rápido você chega.
- Negativa. Já essa correlação é quando se concentram em uma linha decrescente. Conforme uma variável aumenta, a outra diminui
- Curva. É uma combinação de correlação positiva e negativa.Ela se da quando em algum momento, a correlação entre as variaveis começa a se tornar contraria. Em exemplo perfeito é na curva de Leffer, ela determina um ponto ótimo da arrecadação de impostos. Ou seja, acima desse ponto, quanto maior for a alíquota de impostos cobrada pelo governo maior será a propensão de sonegação na economia, fazendo com que a arrecadação caia como consequência
- Parcial. A correlação parcial indica que até determinado momento entre as variaveis, a correlação é positiva ou negativa, mas que após um ponto máximo a correlação se perde.
• A correlação é estatisticamente significativa
Existem duas partes para determinar se a correlação é estatisticamente significativa. A primeira etapa é determinar a equação de “melhor ajuste” entre x e y. A equação de melhor ajuste tem a forma:
y = b 0 + b 1 x
Onde y é o valor previsto de y para um determinado valor de x, b 1 é a inclinação da linha e b 0 é a interceptação y (onde a linha cruza o eixo y).
No nosso exemplo, a linha de melhor ajuste para a Figura 1 é dada por:
y = -0,565x + 53,32
O número chave na equação é -0,565, que é a inclinação da linha. Isso dá a você a mudança em y que é causada por uma mudança em x. Para cada 1 km/h mais rápido que você vá, o tempo para chegar ao trabalho diminuirá em 0,565 minutos, em média.
Mas você não pode simplesmente fazer a linha de melhor ajuste e parar. Qualquer conjunto de dados terá uma linha de melhor ajuste que pode ser adicionada a ele. Isso não significa que o ajuste seja estatisticamente significativo. Para determinar isso, você precisará examinar o valor p do modelo. . Quando você executa uma regressão para determinar a linha de melhor ajuste, geralmente obterá uma saída semelhante à seguinte para a velocidade e o tempo para chegar aos dados de trabalho.
| Coeficiente | Erro padrão | t Stat | valor p | |
|---|---|---|---|---|
| Interceptar | 53,32 | 6,885 | 7,744 | 0,0000 |
| Rapidez | -0,565 | 0,126 | -4,471 | 0,0002 |
Esta tabela ajuda você a decidir se a velocidade tem um impacto significativo no tempo. A coluna a ser observada é a coluna de valor p. Sua suposição inicial é que a velocidade não afeta o tempo para chegar ao trabalho. Se o valor de p for baixo, essa suposição não é boa e a velocidade tem impacto. Um valor de p baixo é normalmente 0,05 ou menos.
Neste exemplo, o valor de p é 0,0002. Isso é baixo e significa que a velocidade tem um impacto estatisticamente significativo no tempo para chegar ao trabalho.
Quando utilizar um Diagrama de Dispersão
- Quando você tiver emparelhado dados numéricos. Esse método é muito útil quando vocês deseja validar a correlação entre uma causa e um único efeito, ou 2 variáveis.
- Variáveis dependentes têm vários valores para cada figura associada à variável independente. Quando isso acontece, você pode usar o diagrama de dispersão para visualizar de forma gráfica esse relacionamento.
- Ao tentar identificar as causas potenciais dos problemas. Por isso o Diagrama de Dispersão é um dos vários métodos de análise de causa raiz. Isso acontece por facilitar o entendimento da correlaçao entre um problema/efeito e uma POSSÍVEL causa. Lembrando que quando você levantar as possíveis causas (usando outro método como o “5 porquês”, “Diagrama de Ishikawa”) você deve analisar o relacionamento entre cada uma delas e o problema (variável independente).
- Depois de fazer um brainstorming de causas e efeitos usando um Diagrama de Ishikawa (ou espinha de peixe). Para determinar objetivamente a relação entre uma causa e um efeito particular.
Como montar um Diagrama de Dispersão
Etapa 1 – Identifique as variáveis para avaliar
O primeiro passo para criar o Diagrama de Dispersão, você precisa determinar e coletar quais serão os dados que vão ser analisado, para a verificação da relação entre eles. Colete pares de dados onde houver suspeita de relacionamento.
Etapa 2 – Desenhe o gráfico
Desenhe o diagrama de dispersão com a variável independente no eixo horizontal (eixo x) e a variável dependente no eixo vertical (eixo y). Para cada par de dados, coloque um ponto ou símbolo onde o valor do eixo x cruza o valor do eixo y.
Importante: Se dois pontos caírem juntos, coloque-os lado a lado, tocando, para que você possa ver os dois.

Por exemplo, na imagem acima, o ponto vermelho representa o par de: eixo x (50) e eixo y (22);
Etapa 3 – Análise o gráfico
Revise o padrão de pontos para determinar se um relacionamento está presente. Se os dados formarem claramente uma linha ou curva, você pode parar. As variáveis são correlacionadas. Você pode querer usar regressão ou análise de correlação agora.
Etapa 4 – Crie um plano de ação
Finalmente, terminamos! Agora que você analisou os dados e construiu seu diagrama de dispersão. Se você identificou que existe uma correlação entre os dados você consegue criar um plano de ação adequado para solucionar o problema.
Como outros métodos com o objetivo de encontrar uma causa e efeito entre dados, ele é tão útil quanto o que você faz com ele, ou seja, depois de analisar o resultado, você precisa colocar a “mão na massa” e usa-lo como guia para desenvolver estratégias para seu negocio.
Correlação vs Causalidade
Nota: Deve-se ter cuidado ao construir um diagrama de dispersão, em que “correlação não implica causalidade”, ou seja, uma relação pode ser identificada entre duas variáveis, porém não deve ser assumido que uma variável está causando um efeito com a outra variável.
Pode haver outras variáveis entrando no processo e impactando os resultados, portanto, é importante controlar e monitorar todas as outras variáveis potenciais, para investigar e compreender totalmente as relações de causa e efeito potenciais identificadas por meio da análise do diagrama de dispersão.
Conclusão
Muitas das ferramentas de análise de causa raiz são projetadas para apontar seus esforços na direção certa e estreitar o escopo desses esforços para ser mais eficaz e mais rápido. Outro efeito colateral ou benefício do uso dessas ferramentas pode vir na forma de construção de consenso entre o time.
Com o Diagrama de Dispersão a grande vantagem é conseguir identificar a correlação entre dados, e como principio, utiliza dados para tomar uma decisão, eliminando o “achismo” muito comum em empresas. Com a correlação identificada, basta criar atividades para desenvolver melhoras no seu processo.
Nota: o diagrama de dispersão não mostra a causa raiz de um problema, por isso, você precisa fazer um exercício antes para identificar o que esta acontecendo e as várias possibilidades de causa para esse efeito. Com isso em mãos, você começa a utilizar o diagrama de dispersão para validar a correlação entre as causas e os efeitos.